Module 1.0 - Mini-ML¶

Model¶

  • Models: parameterized functions.

    • $m(x; \theta)$
    • $x \text{ - input}$
    • $m \text{ - model}$

  • Initial Focus:

    • $\theta \text{ - parameters}$

Specifying Parameters¶

  • Datastructures to specify parameters
  • Requirements
    • Independent of implementation
    • Compositional

Module Example¶

In [2]:
from minitorch import Module, Parameter


class OtherModule(Module):
    pass


class MyModule(Module):
    def __init__(self):
        # Must initialize the super class!
        super().__init__()

        # Type 1, a parameter.
        self.parameter1 = Parameter(15)

        # Type 2, user data
        self.data = 25

        # Type 3. another Module
        self.sub_module = OtherModule()

Module Naming¶

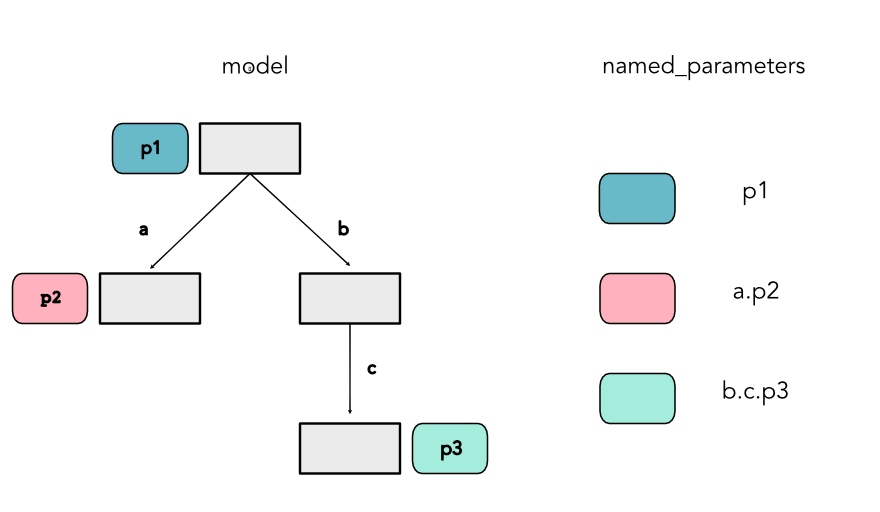
Lecture Quiz¶

Quiz

Outline¶

  • Model

  • Parameters

  • Loss

Datasets¶

Data Points¶

  • Convention $x$
In [3]:
split_graph([s1[0]], [])
Out[3]:

Data Points¶

  • Convention $x$
In [4]:
split_graph([s1[1]], [])
Out[4]:

Data Points¶

  • Convention $x$
In [5]:
split_graph(s1, [])
Out[5]:

Data Labels¶

  • Convention $y$
In [6]:
split_graph([s1[0]], [s2[0]])
Out[6]:

Training Data¶

  • Set of datapoints, each $(x,y)$
In [7]:
split_graph(s1, s2)
Out[7]:

Data Points¶

  • Convention $x$

Data Points¶

  • Convention $x$

Data Set¶

Data Labels¶

  • Convention $y$

Model¶

Models¶

  • Functions from data points to labels
  • Functions $m(x; \theta)$
  • Any function is okay (e.g. Modules)

Example Model¶

  • Example of a simple model

    x = (0.5, 0.2)

In [8]:
@dataclass
class Model:
    def forward(self, x):
        return 0 if x[0] < 0.5 else 1

Model 1¶

  • Linear Model
In [9]:
from minitorch import Parameter, Module
class Linear(Module):
    def __init__(self, w1, w2, b):
        super().__init__()
        self.w1 = Parameter(w1)
        self.w2 = Parameter(w2)
        self.b = Parameter(b)

    def forward(self, x1: float, x2: float) -> float:
        return self.w1.value * x1 + self.w2.value * x2 + self.b.value

Model 1¶

In [10]:
model = Linear(w1=1, w2=1, b=-0.9)
draw_graph(model)
Out[10]:

Model 2¶

In [11]:
class Split:
    def __init__(self, linear1, linear2):
        super().__init__()
        # Submodules
        self.m1 = linear1
        self.m2 = linear2

    def forward(self, x1, x2):
        return self.m1.forward(x1, x2) * self.m2.forward(x1, x2)
In [12]:
model_b = Split(Linear(1, 1, -1.5), Linear(1, 1, -0.5))
draw_graph(model_b)
Out[12]:

Model 3¶

In [13]:
class Part:
    def forward(self, x1, x2):
        return 1 if (0.0 <= x1 < 0.5 and 0.0 <= x2 < 0.6) else 0
In [14]:
draw_graph(Part())
Out[14]:

Parameters¶

Parameters¶

  • Knobs that control the model
  • Any information that controls the model shape

Parameters¶

  • Change $\theta$
In [15]:
show(Linear(w1=1, w2=1, b=-0.5))

show(Linear(w1=1, w2=1, b=-1))
Out[15]:

Linear Parameters¶

a. rotating the linear separator

In [16]:
model1 = Linear(w1=1, w2=1, b=-1.0)
model2 = Linear(w1=0.5, w2=1.5, b=-1.0)
In [17]:
compare(model1, model2)
Out[17]:
→

Linear Parameters¶

b. changing the separator cutoff

In [18]:
model1 = Linear(w1=1, w2=1, b=-1.0)
model2 = Linear(w1=1, w2=1, b=-1.5)
In [19]:
compare(model1, model2)
Out[19]:
→

Math¶

  • Linear Model

$$m(x; w, b) = x_1 \times w_1 + x_2 \times w_2 + b $$

In [20]:
def forward(self, x1: float, x2: float) -> float:
    return self.w1 * x1 + self.w2 * x2 + self.b

Loss¶

What is a good model?¶

In [21]:
hcat([show(Linear(1, 1, -1.0)), show(Linear(1, 1, -0.5))], 0.3)
Out[21]:

Distance¶

  • $|m(x)|$ correct or incorrect
In [22]:
with_points(s1, s2, Linear(1, 1, -0.4))
Out[22]:

Points¶

In [23]:
pts = [
    with_points([s1[0]], [], Linear(1, 1, -1.5)),
    with_points([s1[0]], [], Linear(1, 1, -1)),
    with_points([s1[0]], [], Linear(1, 1, -0.5)),
]
hcat(pts, 0.3)
Out[23]:

Loss¶

  • Loss weights our incorrect points
  • Uses distance from boundary

$L(w_1, w_2, b)$ is loss, function of parameters.

Warmup: ReLU¶

In [24]:
def point_loss(m_x):
    return minitorch.operators.relu(m_x)
In [25]:
graph(point_loss, [], [])
Out[25]:

Loss of points¶

In [26]:
graph(point_loss, [], [-2, -0.2, 1])
Out[26]:

Loss of points¶

In [27]:
graph(lambda x: point_loss(-x), [-1, 0.4, 1.3], [])
Out[27]:

Full Loss¶

In [28]:
def full_loss(m):
    l = 0
    for x, y in zip(s.X, s.y):
        l += point_loss(-y * m.forward(*x))
    return -l

Point Loss¶

In [30]:
graph(point_loss, [], [])
Out[30]:
In [31]:
graph(point_loss, [], [-2, -0.2, 1])
Out[31]:

What is a good model?¶

In [32]:
hcat([show(Linear(1, 1, -1.0)), show(Linear(1, 1, -0.5))], 0.3)
Out[32]:

Sigmoid Function¶

In [33]:
graph(minitorch.operators.sigmoid, width=8).scale_x(0.5)
Out[33]:

Playground¶

Playground

Q&A¶