Module 1.2 - Autodifferentiation¶
Symbolic Derivative¶
$$f(x) = \sin(2 x) \Rightarrow f'(x) = 2 \cos(2 x)$$
In [2]:
plot_function("f'(x) = 2*cos(2x)", lambda x: 2 * math.cos(2 * x))
Derivatives with Multiple Arguments¶
$$f_x'(x, y) = \cos(x) \ \ \ f_y'(x, y) = -2 \sin(y)$$
In [3]:
plot_function3D("f'_x(x, y) = cos(x)", lambda x, y: math.cos(x))
Review: Derivative¶
$$f(x) = x^2 + 1$$
In [4]:
def f(x):
return x * x + 1.0
plot_function("f(x)", f)
Review: Derivative¶
$$f'(x) = 2x$$
In [5]:
def d_f(x):
return 2 * x
def tangent_line(slope, x, y):
def line(x_):
return slope * (x_ - x) + y
return line
plot_function("f(x) vs f'(2)", f, fn2=tangent_line(d_f(2), 2, f(2)))
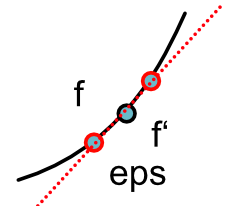
Numerical Derivative: Central Difference¶
Approximate derivatative
$$f'(x) \approx \frac{f(x + \epsilon) - f(x-\epsilon)}{2\epsilon}$$
Derivative as higher-order function¶
$$f(x) = ...$$ $$f'(x) = ...$$
In [6]:
def derivative(f: Callable[[float], float]) -> Callable[[float], float]:
def f_prime(x: float) -> float: ...
return f_prime
Quiz¶
Outline¶
- Autodifferentiation
- Computational Graph
- Backward
- Chain Rule
Autodifferentiation¶
Goal¶
- Write down arbitrary code
- Transform to compute deriviative
- Use this to fit models
How does this differ?¶
- Are these symbolic derivatives?
- No, don't get out mathematical form
- Are these numerical derivatives?
- No, don't use local evaluation.
Overview: Autodifferentiation¶
- Forward Pass - Trace arbitrary function
- Backward Pass - Compute derivatives of function
Forward Pass¶
- User writes mathematical code
- Collect results and computation graph
In [ ]:
In [7]:
draw_boxes([("", ""), "", ("", ""), ""], [1, 2, 1], lr=True)
Out[7]:
Backward Pass¶
- Minitorch uses graph to compute derivative 1, 2,
In [8]:
backprop(6)
Out[8]:
Example : Linear Model¶
- Our forward computes
$${\cal L}(w_1, w_2, b) = \text{ReLU}(m(x;w, b))$$ where
$$m(x; w_1, w_2, b) = x_1 \times w_1 + x_2 \times w_2 + b$$
- Our backward computes
$${\cal L}'_{w_1}(w_1, w_2, b) \ \ {\cal L}'_{w_2}(w_1, w_2, b) \ \ {\cal L}'_b(w_1, w_2, b)$$
Derivative Checks¶
- Property: All three of these should roughly match
Strategy¶
- Replace generic numbers.
- Replace mathematical functions.
- Track with functions have been applied.
Computation Graph¶
Strategy¶
- Act like a numerical value to user
- Trace the operations that are applied
- Hide access to internal storage
Box Diagrams¶
$$f(x) = \text{ReLU}(x)$$
In [9]:
draw_boxes(["$x_2$", "$f(x_2)$"], [1]).center_xy().scale_uniform_to_x(1).with_envelope(
chalk.rectangle(1, 0.5)
)
Out[9]:
Box Diagrams¶
$$f(x, y) = x \times y$$
In [10]:
draw_boxes([("$x$", "$y$"), "$f(x, y)$"], [1]).center_xy().scale_uniform_to_x(
1
).with_envelope(chalk.rectangle(1, 0.5))
Out[10]:
Code Demo¶
How does this work¶
- Arrows are intermediate values
- Boxes are function application
$$f(x) = \text{ReLU}(x)$$ $$g(x) = \log(x) $$
In [11]:
draw_boxes(["$x$", "$g(x)$", "$f(g(x))$"], [1, 1]).center_xy().scale_uniform_to_x(
1
).with_envelope(chalk.rectangle(1, 0.5))
Out[11]:
Implementation¶
Functions¶
- Functions are implemented as static classes
- We implement hidden
forwardandbackwardmethods - User calls
applywhich handles wrapping / unwrapping
Functions¶
$$f(x) = x \times 5$$
In [12]:
draw_boxes(["$x_1$", "$f(x_1)$"], [1]).center_xy().scale_uniform_to_x(1).with_envelope(
chalk.rectangle(1, 0.5)
)
Out[12]:
In [13]:
class TimesFive(ScalarFunction):
@staticmethod
def forward(ctx: Context, x: float) -> float:
return x * 5
Multi-arg Functions¶
In [14]:
draw_boxes([("$x$", "$y$"), "$f(x, y)$"], [1]).center_xy().scale_uniform_to_x(
1
).with_envelope(chalk.rectangle(1, 0.5))
Out[14]:
In [15]:
class Mul(ScalarFunction):
@staticmethod
def forward(ctx: Context, x: float, y: float) -> float:
return x * y
Variables¶
- Wrap a numerical value
In [16]:
x_1 = Scalar(10.0)
x_2 = Scalar(0.0)
Using scalar variables.¶
In [17]:
x = Scalar(10.0)
z = TimesFive.apply(x)
def apply(cls, val: Scalar) -> Scalar:
...
unwrapped = val.data
new = cls.forward(unwapped)
return Scalar(new)
...
Multiple Steps¶
In [18]:
draw_boxes(["$x$", "$g(x)$", "$f(g(x))$"], [1, 1]).center_xy().scale_uniform_to_x(
1
).with_envelope(chalk.rectangle(1, 0.3))
Out[18]:
In [19]:
x = Scalar(10.0)
y = Scalar(5.0)
z = TimesFive.apply(x)
out = TimesFive.apply(z)
Tricks¶
- Use operator overloading to ensure that functions are called
In [20]:
out2 = x * y
def __mul__(self, b: Scalar) -> Scalar:
return Mul.apply(self, b)
- Many functions e.g.
subcan be implemented with other calls.
Notes¶
- Since each operation creates a new variable, there are no loops.
- Cannot modify a variable. Graph only gets larger.
Backwards¶
How do we get derivatives?¶
- Base case: compute derivatives for single functions
- Inductive case: define how to propagate a derivative
Base Case: Coding Derivatives¶
- For each $f$ we need to also provide $f'$
- This part can be done through manual symbolic differentiation
In [21]:
# TODO!
draw_boxes(["", "", ("", ""), ""], [1, 1], lr=False).center_xy().scale_uniform_to_x(
1
).with_envelope(chalk.rectangle(1, 0.3))
Out[21]:
Code¶
- Backward use $f'$
- Returns $f'(x) \times d$
In [22]:
class TimesFive(ScalarFunction):
@staticmethod
def forward(ctx, x: float) -> float:
return x * 5
@staticmethod
def backward(ctx, d: float) -> float:
f_prime = 5
return f_prime * d
Two Arg¶
- What about $f(x, y)$
- Returns $f'_x(x,y) \times d$ and $f'_y(x,y) \times d$
In [23]:
draw_boxes([("", ""), ""], [1], lr=False).center_xy().scale_uniform_to_x(
1
).with_envelope(chalk.rectangle(1, 0.5))
Out[23]:
Code¶
In [24]:
class AddTimes2(ScalarFunction):
@staticmethod
def forward(ctx, x: float, y: float) -> float:
return x + 2 * y
@staticmethod
def backward(ctx, d) -> Tuple[float, float]:
return d, 2 * d
What is Context?¶
- Context on
forwardis given tobackward - May be called at different times.
Context¶
Consider a function Square
- $g(x) = x^2$ that squares x
- Derivative function uses variable $g'(x) = 2 \times x$
- However backward doesn't take args
In [25]:
def backward(ctx, d_out): ...
Context¶
Arguments to backward must be saved in context.
In [26]:
class Square(ScalarFunction):
@staticmethod
def forward(ctx: Context, x: float) -> float:
ctx.save_for_backward(x)
return x * x
@staticmethod
def backward(ctx: Context, d_out: float) -> Tuple[float, float]:
x = ctx.saved_values
f_prime = 2 * x
return f_prime * d_out
Context Internals¶
Run Square
In [27]:
x = minitorch.Scalar(10)
x_2 = Square.apply(x)
x_2.history
Out[27]:
ScalarHistory(last_fn=<class '__main__.Square'>, ctx=Context(no_grad=False, saved_values=(10.0,)), inputs=[Scalar(10.0)])