Module 3.0 - Real Neural Networks

Map Gradient

Example: Tensor Inversion

• $G^{i}(x) = 1 / x_i$

• $G'^{i}_{x_i}(x) = -(x_i)^{-2}$

• $f'_{x_i}(G(x)) = -(x_i)^{-2} * d_i$

Example: Inv

class Inv(minitorch.Function):
    @staticmethod
    def forward(ctx, t1: Tensor) -> Tensor:
        ctx.save_for_backward(t1)
        return t1.f.inv_map(t1)

    @staticmethod
    def backward(ctx, d: Tensor) -> Tensor:
        (t1,) = ctx.saved_values
        return d.f.inv_back_zip(t1, d)

Example: Multiplicaiton

• $G^{i}(x, y) = x_i * y_i$

• $G'^{i}_{x_i}(x, y) = y_i$

• $f'_{x_i}(G(x, y)) = y_i * d_i$

Example: Mult

class Mul(minitorch.Function):
    @staticmethod
    def forward(ctx, t1: Tensor, t2:Tensor) -> Tensor:
        ctx.save_for_backwards((t1, t2))
        return t1.f.mul_map(t1, t2)

    @staticmethod
    def backward(ctx, d: Tensor) -> Tensor:
        (t1, t2) = ctx.saved_values
        return d.f.mul_map(t2, d), d.f.mul_map(t1, d)

Example: Sum

• $G(x) = \sum_i x_i$

• $G'_{x_i}(x) = 1$

• $f'_{x_i}(G(x)) = d$

Reduce Gradient

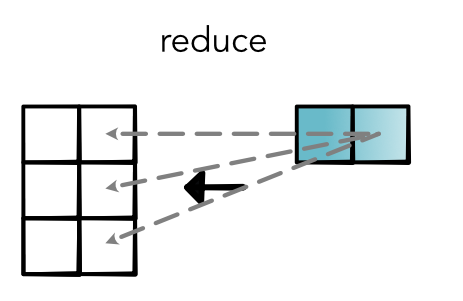
Quiz

Outline

• Training
• Simple NLP

Training

Model: Math

$$ \begin{eqnarray*} \text{lin}(x; w, b) &=& x_1 \times w_1 + x_2 \times w_2 + b \\ h_ 1 &=& \text{ReLU}(\text{lin}(x; w^0, b^0)) \\ h_ 2 &=& \text{ReLU}(\text{lin}(x; w^1, b^1))\\ m(x) &=& \text{lin}(h; w, b) \end{eqnarray*} $$

Simple Dataset

split_graph(s1, s2)

Parameter Fitting

1. Compute the loss function, $\mathcal{L}(\theta)$
2. See how small changes would change the loss
3. Update to parameters to locally reduce the loss

Batching

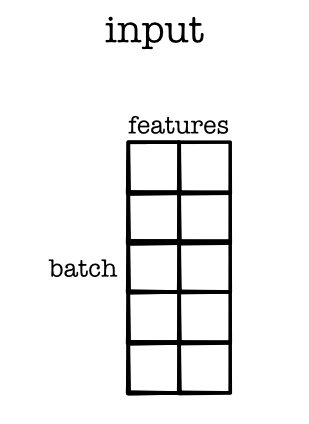
How to Compute Loss

# X - (BATCH, FEATURES)
out = model.forward(X)

# out - (BATCH)
l = loss(out)

# l - (1)

Model: Code

class Network(minitorch.Module):
  def __init__(self):
    ...
    self.layer1 = Linear(FEATURES, HIDDEN)
    self.layer2 = Linear(HIDDEN, HIDDEN)
    self.layer3 = Linear(HIDDEN, 1)

Layer 1: Weight

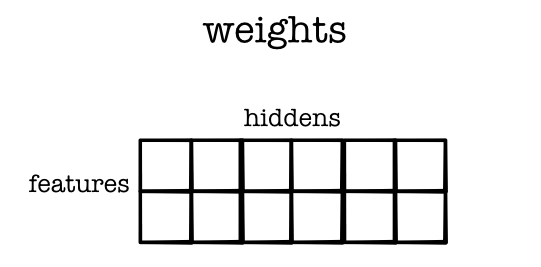
Layer 1: Bias

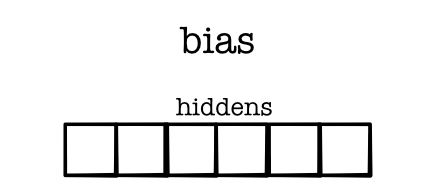
Linear Model

• Use broadcasting to implement the linear function
• Sizes
  • X - (BATCH, FEATURES)
  • weight - (FEATURES, HIDDEN)
  • bias - (HIDDEN)

How Much Does it Cost?

• Counting the operations
• Counting the memory

Layer 2: Weights

Compute Derivatives

Step 2

loss.backward()
print(model.layer1.w_1.value.grad)

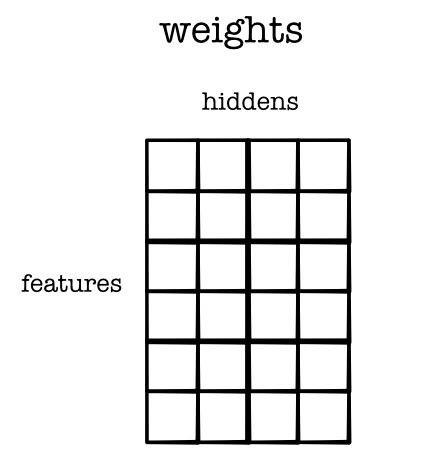
Layer 1: Weight Grad

Update Parameters

Step 3

for p in model.parameters():
  if p.value.grad is not None:
    p.update(p.value - RATE * (p.value.grad / float(data.N)))

Broadcasting

• Batches
• Loss Computation
• Linear computation
• Autodifferentiation
• Gradient updates

Observations

• Exactly the same function as Module-1
• No loops within tensors

Simple NLP

Sentiment Classification

• Canonical sentence classification problem
• Given sentence predict sentiment class
• Key aspects: word polarity

Data

What is a word?

• Treat words as index in vocabulary
• Represent as a one-hot vector

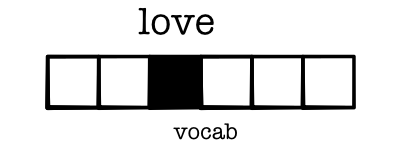
Layer 1

• First layers is called an embedding

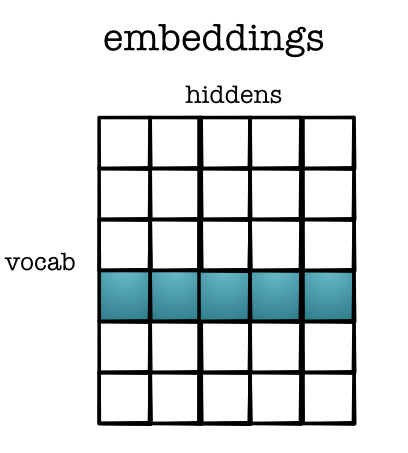
Hidden vector for word

Get word vector

word_one_hot = tensor([0 if i != word else 1
                       for i in range(VOCAB)])
embedding = (layer1 * word_one_hot).sum(1)

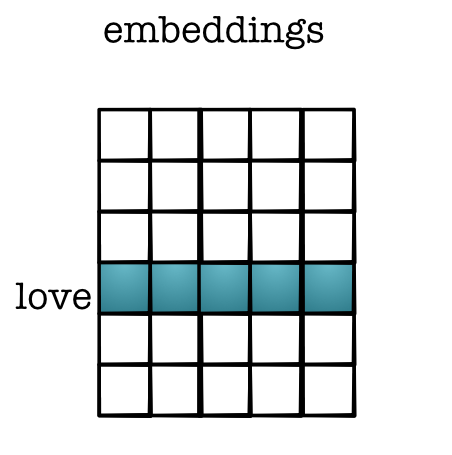
How does this share information?

• Similar words have similar embedding dim
• Dot-product - easy way to tell similarity

(word_emb1 * word_emb2).sum()

• Differentiable!

Where do these come from?

• Trained from a different model
• Extracted and posted to use
• (Many more details in NLP class)

Examples

Embeddings

embedding.weights.value.update(pretrained_weights)

• https://projector.tensorflow.org/

Examples

Query 1

   ^(lisbon|portugal|america|washington|rome|athens|london|england|greece|italy)$

Query 2

  ^(doctor|patient|lawyer|client|clerk|customer|author|reader)$

Sentence Length

• Examples may be of different length
• Need to all be converted to vectors and utilized

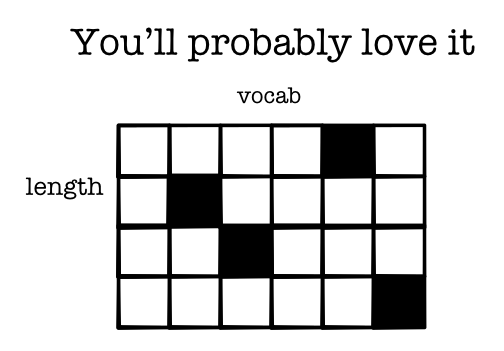
Value Transformation

• batch x length x vocab
• batch x length x feature
• batch x feature
• batch x hidden
• batch

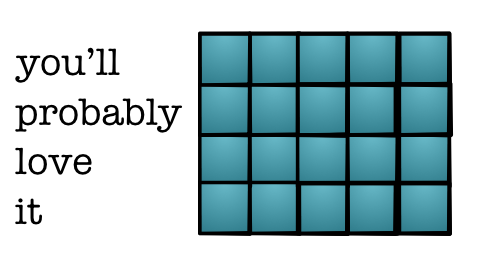
Pooling

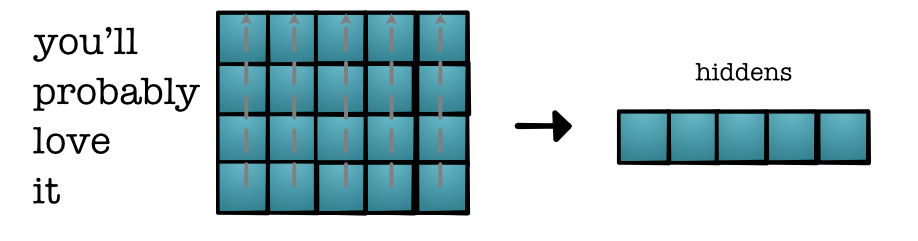
Benefits

• Extremely simple
• Embeddings encode key information
• Have all the tools we need

Full Model

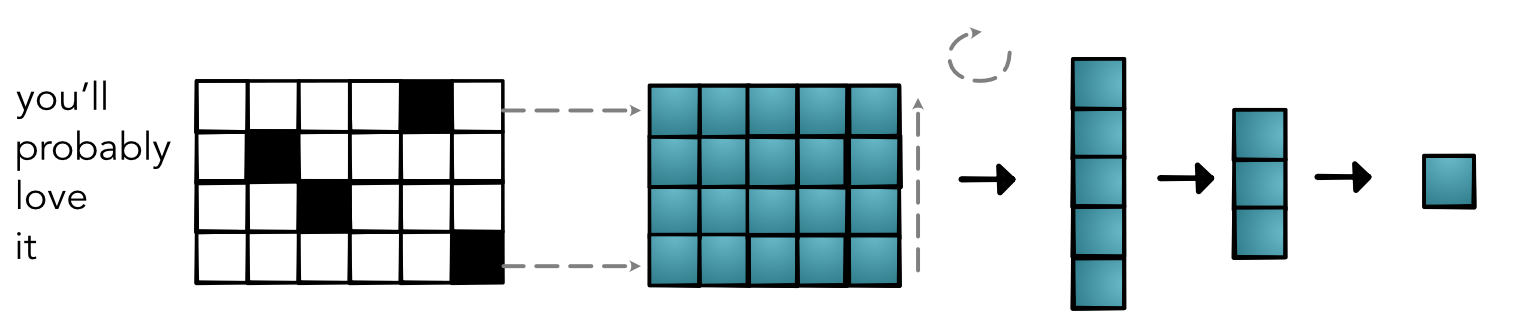
Issues

• Ignores relative order
• Ignores absolute order
• Embeddings for all words, even rare ones