Module 3.3 - CUDA: Memory¶


Thread Names¶
Printing code
@cuda.jit()
def printer(a):
print(cuda.threadIdx.x, cuda.threadIdx.y)
a[:] = 10 + 50
a = np.zeros(10)
printer[1, (10, 10)](a)
`

Thread Names¶
def printer(a):
print(cuda.blockIdx.x,
cuda.threadIdx.x, cuda.threadIdx.y)
a[:] = 10 + 50
a = np.zeros(10)
printer[10, (10, 10)](a)
What's my name?¶
BLOCKS_X = 32
BLOCKS_Y = 32
THREADS_X = 10
THREADS_Y = 10
def fn(a):
x = cuda.blockIdx.x * THREADS_X + cuda.threadIdx.x
y = cuda.blockIdx.y * THREADS_Y + cuda.threadIdx.y
fn = cuda.jit()(fn)
fn[(BLOCKS_X, BLOCKS_Y), (THREADS_X, THREADS_Y)](a)
Stack¶
- Threads: Run the code
- Block: Groups "close" threads
- Grid: All the thread blocks
- Total Threads:
threads_per_blockxtotal_blocks
Simple Map¶
BLOCKS_X = 32
THREADS_X = 32
@cuda.jit()
def fn(out, a):
x = cuda.blockIdx.x * THREADS_X + cuda.threadIdx.x
if x < a.size:
out[x] = a[x] + 10
fn[BLOCKS_X, THREADS_X](out, a)
Quiz ¶
Outline¶
- Memory
- Example: Slides
- Example: Reduction
Memory¶
Names¶
- Why do the names matter?
- Determine communication
- Locality is key for speed.
Memory¶
- CUDA memory hierarchy
- Local > Shared > Global
- Goal: minimize global reads and writes
Example¶
@cuda.jit()
def local_fn(out, a):
i = cuda.threadIdx.x
local = cuda.local.array(10, numba.int32)
local[0] = 10
local[5] = local[0] + 10
out[i] = local[5]
local_fn[BLOCKS, THREADS](out, a)
out
Constraints¶
- Memory must be typed
- Memory must be constant size
- Memory must be relatively small
BAD Example¶
def local_fn(out, a):
local = cuda.local.array(a.size, numba.int32)
local[0] = 10
local[5] = 20
local_fn = cuda.jit()(local_fn)
local_fn[BLOCKS, THREADS](out, a)
GOOD Example¶
CONSTANT = 10
def block_fn(out, a):
shared = cuda.local.array(CONSTANT, numba.int32)
shared[0] = 10
shared[5] = 20
block_fn = cuda.jit()(block_fn)
block_fn[BLOCKS, THREADS](out, a)
`
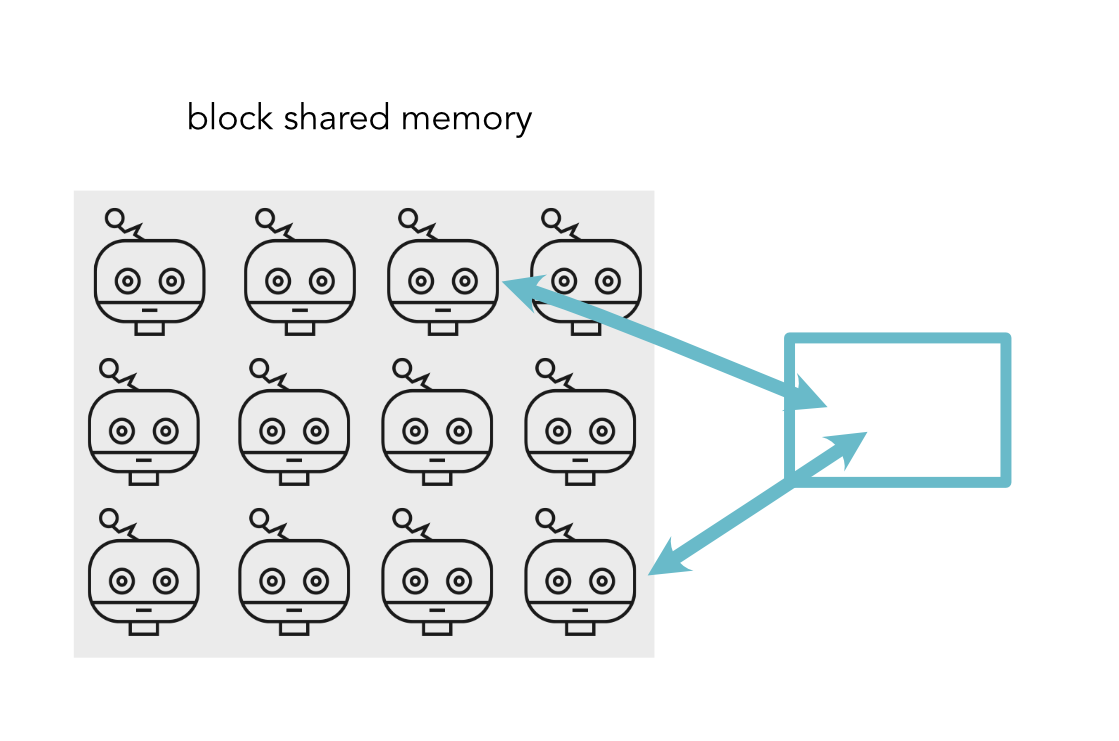
Communication¶
- Threads in a block have shared memory
- Need to
syncto ensure it is written before you read
Shared Example¶
@cuda.jit()
THREADS = 10
def block_fn(out, a):
shared = cuda.shared.array(THREADS, numba.int32)
i = cuda.threadIdx.x
shared[i] = a[i]
cuda.syncthreads()
out[i+1 % THREADS] = shared[i]
block_fn[1, THREADS](out, a)
Constraints¶
- Memory must be typed
- Memory must be constant size
- Memory must be relatively small
Algorithms¶
Thinking about Speed¶
- Algorithms: Reduce computation complexity
- Typical: Remove loops, code operations
Sliding Average¶
Compute sliding average over a list
sub_size = 2
a = [4, 2, 5, 6, 2, 4]
out = [3, 3.5, 5.5, 4, 3]
Local Sum¶
Compute sliding average over a list
def slide_py(out, a):
for i in range(out.size):
out[i] = 0
for j in range(sub_size):
out[i] += a[i + j]
out[i] = out[i] / sub_size
Planning for CUDA¶
- Count up the memory accesses
- How many global / shared / local reads?
- Can we make move things to be more local?
Basic CUDA¶
@cuda.jit
def slide_cuda(out, a):
i = cuda.threadIdx.x
if i + sub_size < a.size:
out[i] = 0
for j in range(sub_size):
out[i] += a[i + j]
out[i] = out[i] / sub_size
Planning for CUDA¶
sub_sizeglobal reads per threadsub_sizeglobal writes per thread- Each is being read too many times.
Strategy¶
- Use blocks to move from global to shared
- Use thread to move from shared to local
Better CUDA¶
One global write per thread
@cuda.jit()
def slide_cuda(out, a):
i = cuda.threadIdx.x
if i + sub_size < a.size:
temp = 0
for j in range(sub_size):
temp += a[i + j]
out[i] = temp / sub_size
Pattern¶
Copy from global to shared
local_idx = cuda.threadIdx.x
shared[local_idx] = a[i]
cuda.syncthreads()
Better CUDA¶
@cuda.jit
def slide_cuda(out, a):
shared = cuda.shared.array(THREADS + sub_size)
i = cuda.threadIdx.x
if i + sub_size < a.size:
shared[i] = a[i]
if i < sub_size and i + THREADS < a.size:
shared[i + THREADS] = a[i + THREADS]
cuda.syncthreads()
temp = 0
for j in range(sub_size):
temp += shared[i + j]
out[i] = temp / sub_size
Counts¶
- Significantly reduced global reads and writes
- Needed block shared memory to do this
Example 2: Reduction¶
Compute sum reduction over a list
a = [4, 2, 5, 6, 1, 2, 4, 1]
out = [26]
Algorithm¶
- Parallel Prefix Sum Computation
- Form a binary tree and sum elements
Associative Trick¶
Formula $$a = 4 + 2 + 5 + 6 + 1 + 2 + 4 + 1$$ Same as $$a = (((4 + 2) + (5 + 6)) + ((1 + 2) + (4 + 1)))$$
Associative Trick¶
Round 1 $$a = (((4 + 2) + (5 + 6)) + ((1 + 2) + (4 + 1)))$$ Round 2 $$a = ((6 + 11) + (3 + 5))$$ Round 3 $$a = (17 + 8)$$ Round 4 $$a = 25$$
Thread Assignments¶
Round 1 (4 threads needed, 8 loads) $$a = (((4 + 2) + (5 + 6)) + ((1 + 2) + (4 + 1)))$$
Round 2 (2 threads needed, 4 loads) $$a = ((6 + 11) + (3 + 5))$$ Round 3 (1 thread needed, 2 loads) $$a = (17 + 8)$$ Round 4 $$a = 25$$
Open Questions¶
- When do we read / write from global memory?
- Where do we store the intermediate terms?
- Which threads work and which do nothing?
- How does this work with tensors?
Table¶
| Thread 0 | Thread 1 | Thread 2 | Thread 3 |
|----------|-----------|----------|----------|
| 4 + 2 | 5 + 6 | 1 + 2 | 4 + 1 |
| 6 + 11 | (zzz) | 3 + 5 | (zzz) |
| 17 + 18 | (zzz) | (zzz) |(zzz) |Harder Questions¶
- What if the sequence is too short?
- What if the sequence is too long?
Too Short - Padding¶
- Recall that we always have a
start, e.g. 0 - Can pad our sequence with
start - In practice can be done by initializing shared memory.
Too Long - Multiple Runs¶
Sequence may have more elements than our block.
Do not want to share values between of blocks.
However, can run the code multiple times.
Example - Long Sequence¶
Formula $$a = 4 + 2 + 5 + 6 + 1 + 2 + 4 + 1 + 10$$ Block size 8 $$a = (((4 + 2) + (5 + 6)) + ((1 + 2) + (4 + 1))) + 10$$