Module 4.3 - Advanced NNs¶

"Pooling"¶

Reduction applied to each region:

Simple Implementation¶

  • Ensure that it is contiguous
  • Use View to "fold" the tensor

Why does folding work?¶

  • View requires "contiguous" tensor
  • View(4, 2) makes strides (2, 1)

Simple Implementation¶

  • Reduce along created fold

Quiz¶

Gradient Flow¶

  • Layers that are used get more updates
  • Gradient signals which aspect was important
  • Can have extra layers

More Reductions¶

  • Heading for a max reduction
  • Heading for a softmax output
  • Quick detour

ReLU, Step, Sigmoid¶

Basic Operations¶

  • Introduced in Module-0
  • Widely used in ML
  • What is it?

Simple Function: ReLU¶

Main "activation" function

Primarily used to split the data.

Simple Function: Step¶

Step function $f(x) = x > 0$ determines correct answer

ReLU¶

Mathematically,

$$\text{ReLU}(x) = \max\{0, x\}$$

Simplest max function.

Step¶

Mathematically,

$$\text{step}(x) = x > 0 = \arg\max\{0, x\}$$

Simplest argmax function.

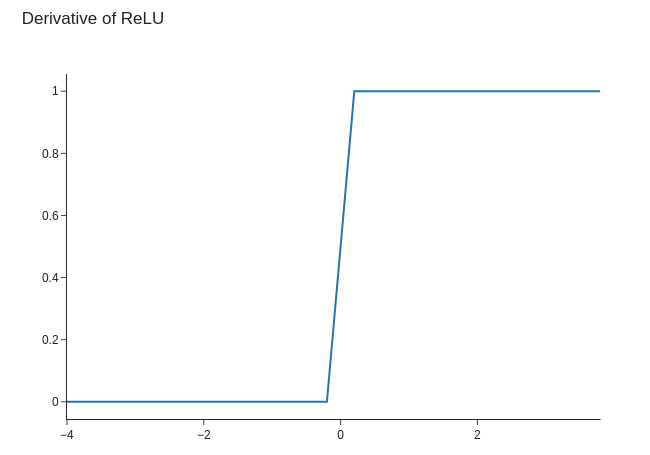
Relationship¶

Step is derivative of ReLU

$$ \begin{eqnarray*} \text{ReLU}'(x) &=& \begin{cases} 0 & \text{if } x \leq 0 \\ 1 & \text{ow} \end{cases} \\ \text{step}(x) &=& \text{ReLU}'(x) \end{eqnarray*} $$

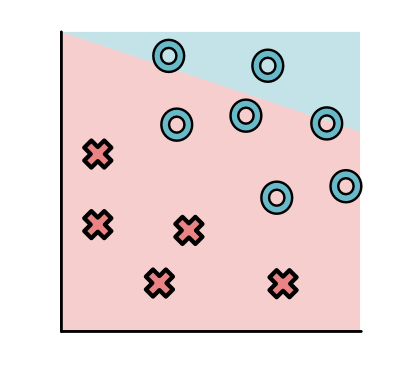
Loss of step tells us how many points are wrong.

Derivative of Step?¶

Mathematically,

$$\text{step}'(x) = \begin{cases} 0 & \text{if } x \leq 0 \\ 0 & \text{ow} \end{cases}$$

Not a useful function to differentiate

Altenative Function: Sigmoid¶

Used to determine the loss function

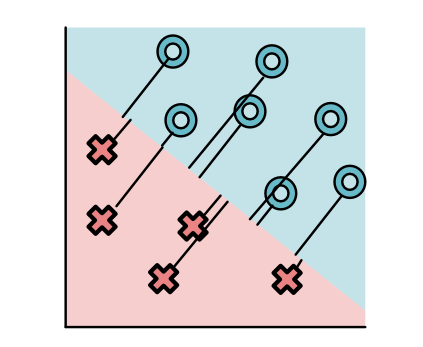
Soft (arg)max?¶

Would be nice to have a version that with a useful derivative

$$\text{sigmoid}(x) = \text{softmax} \{0, x\}$$

Useful soft version of argmax.

Max, Argmax, Softmax¶

Challenge¶

How do we generalize sigmoid to multiple outputs?

Max reduction¶

  • Max is a binary associative operator

  • $\max(a, b)$ returns max value

  • Generalized $\text{ReLU}(a) = \max(a, 0)$

Max Pooling¶

  • Common to apply pooling with max
  • Sets pooled value to "most active" in block
  • Forward code is easy to implement

Max Backward¶

  • Unlike sum, max throws away other values
  • Only top value gets used
  • Backward needs to know this.

Argmax¶

  • Function that returns argmax, one-hot
  • Generalizes step

Max Backward¶

  • First compute argmax
  • Only send gradient to argmax gradinput
  • Everything else is 0

Ties¶

  • What if there are two or more argmax's?
  • Max is non-differentiable, like ReLU(0).
  • Short answer: Ignore, pick one

HW¶

  • When writing tests for max, ties will break finite-differences
  • Suggestion: perturb your input by adding a small amount of random noise.

Soft argmax?¶

  • Need a soft version of argmax.
  • Generalizes sigmoid for our new loss function
  • Standard name -> softmax

Softmax¶

$$\text{softmax}(\textbf{x}) = \frac{\exp \textbf{x}}{\sum_i \exp x_i}$$

Sigmoid is Softmax¶

$$\text{softmax}([0, x])[1] = \frac{\exp x}{\exp x + \exp 0} = \sigma(x)$$

Softmax¶

Softmax

Review¶

  • ReLU -> Max
  • Step -> Argmax
  • Sigmoid -> Softmax

Softmax¶

Network¶

Network

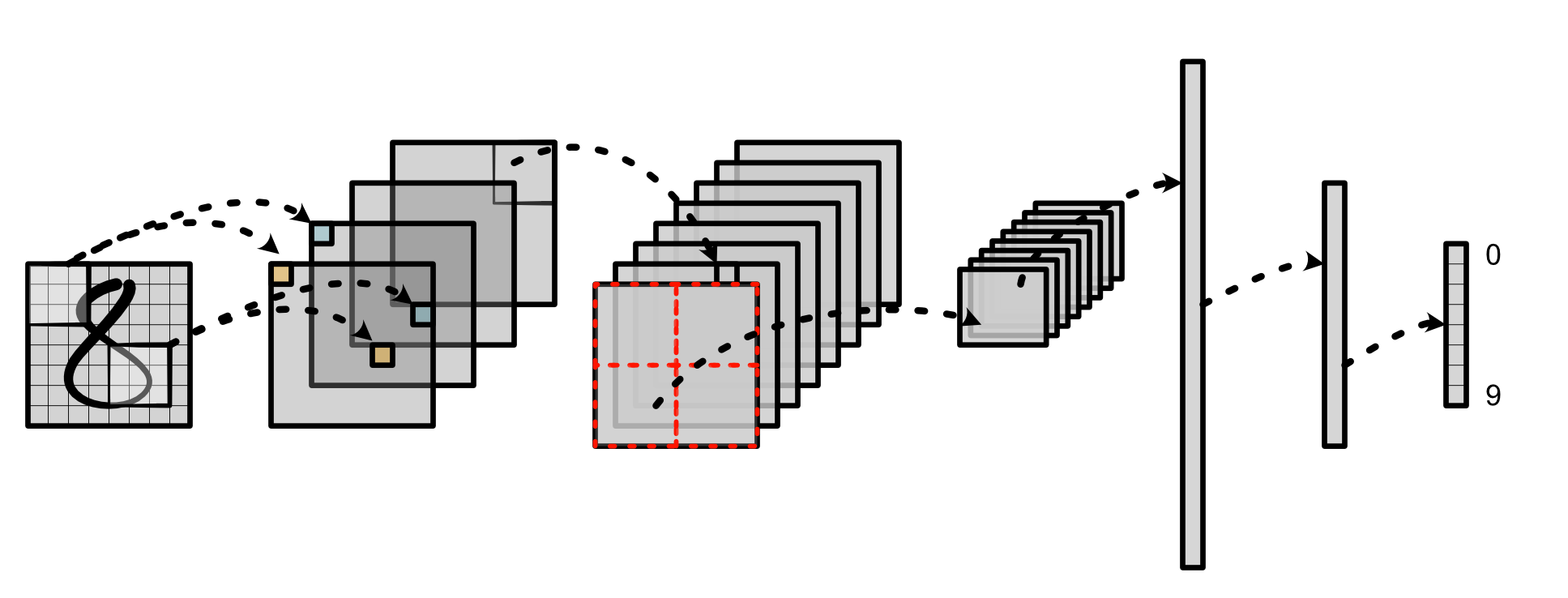
Softmax Layer¶

  • Produces a probability distribution over outputs (Sum to 1)
  • Derivative similar to sigmoid
  • Lots of interesting practical properties

Softmax in Context¶

  • Not a map!
  • Gradient spreads out from one point to all.

Softmax¶

  • (Colab)[https://colab.research.google.com/drive/1EB7MI_3gzAR1gFwPPO27YU9uYzE_odSu]

Soft Gates¶

New Methods¶

  • Sigmoid and softmax produce distributions
  • Can be used to "control" information flow

Example¶

Returns a combination of x and y $$f(x, y, r) = x * \sigma(r) + y * (1 - \sigma(r))$$

Gradient is controlled¶

$$\begin{eqnarray*} f'_x(x, y, r) &= \sigma(r) \\ f'_y(x, y, r) &= (1 - \sigma( r))\\ f'_r(x, y, r) &= (x - y) \sigma'(r) \end{eqnarray*}$$

Neural Network Gates¶

Learn which one of the previous layers is most useful. $$\begin{eqnarray*} r &= NN_1 \\ x &= NN_2 \\ y &= NN_3\\ \end{eqnarray*} $$

Gradient Flow¶

  • Layers that are used get more updates
  • Gradient signals which aspect was important
  • Can have extra layers

Selecting Choices¶

  • Gating gives us a binary choice
  • What if we want to select between many elements?
  • Softmax!

Softmax Gating¶

Combines many elements of X based on R

$$f(X, R) = X \times softmax(R)$$

Softmax Gating¶

  • Brand name: Attention

Example: Translation¶

  • Show example

Example: GPT-3¶

  • Show example

QA¶