Tensors

We now have a fully developed autodifferentiation system built around scalars. This system is correct, but you saw during training that it is inefficient. Every scalar number requires building an object, and each operation requires storing a graph of all the values that we have previously created. Training requires repeating the above operations, and running models, such as a linear model, requires a for loop over each of the terms in the network.

This module introduces and implements a tensor object that will solve these problems. Tensors group together many repeated operations to save Python overhead and to pass off grouped operations to faster implementations.

Guides

For this module we have implemented the skeleton tensor.py file for you. This is similar in spirit to scalar.py from the last assignment. Before starting, it is worth reading through this file to have a sense of what a Tensor does. Each of the following tasks asks you to implement the methods this file relies on:

tensor.py : User facing interface to tensor
tensor_data.py : Indexing, strides, and storage
tensor_ops.py : Higher-order tensor operations
tensor_functions.py : Autodifferentiation-ready functions

Tasks 2.1: Tensor Data - Indexing

The MiniTorch library implements the core tensor backend as minitorch.TensorData. This class handles indexing, storage, transposition, and low-level details such as strides. You will first implement these core functions before turning to the user-facing class minitorch.Tensor.

Todo

Complete the following functions in minitorch/tensor_data.py, and pass tests marked as task2_1.

`minitorch.index_to_position(index: Index, strides: Strides) -> int`

Converts a multidimensional tensor index into a single-dimensional position in storage based on strides.

Parameters:

index –

index tuple of ints
strides –

tensor strides

Returns:

int –

Position in storage

`minitorch.to_index(ordinal: int, shape: Shape, out_index: OutIndex) -> None`

Convert an ordinal to an index in the shape. Should ensure that enumerating position 0 ... size of a tensor produces every index exactly once. It may not be the inverse of index_to_position.

Parameters:

ordinal (int) –

ordinal position to convert.
shape –

tensor shape.
out_index –

return index corresponding to position.

`minitorch.TensorData.permute(*order: int) -> TensorData`

Permute the dimensions of the tensor.

Parameters:

*order (int, default: () ) –

a permutation of the dimensions

Returns:

TensorData –

New TensorData with the same storage and a new dimension order.

Tasks 2.2: Tensor Broadcasting

Todo

Complete following functions in minitorch/tensor_data.py and pass tests marked as task2_2.

`minitorch.shape_broadcast(shape1: UserShape, shape2: UserShape) -> UserShape`

Broadcast two shapes to create a new union shape.

Parameters:

shape1 –

first shape
shape2 –

second shape

Returns:

UserShape –

broadcasted shape

Raises:

IndexingError –

if cannot broadcast

`minitorch.broadcast_index(big_index: Index, big_shape: Shape, shape: Shape, out_index: OutIndex) -> None`

Convert a big_index into big_shape to a smaller out_index into shape following broadcasting rules. In this case it may be larger or with more dimensions than the shape given. Additional dimensions may need to be mapped to 0 or removed.

Parameters:

big_index –

multidimensional index of bigger tensor
big_shape –

tensor shape of bigger tensor
shape –

tensor shape of smaller tensor
out_index –

multidimensional index of smaller tensor

Returns:

None –

None

Tasks 2.3: Tensor Operations

Tensor operations apply high-level, higher-order operations to all elements in a tensor simultaneously. In particular, you can map, zip, and reduce tensor data objects together. On top of this foundation, we can build up a Function class for Tensor, similar to what we did for the ScalarFunction. In this task, you will first implement generic tensor operations and then use them to implement forward for specific operations.

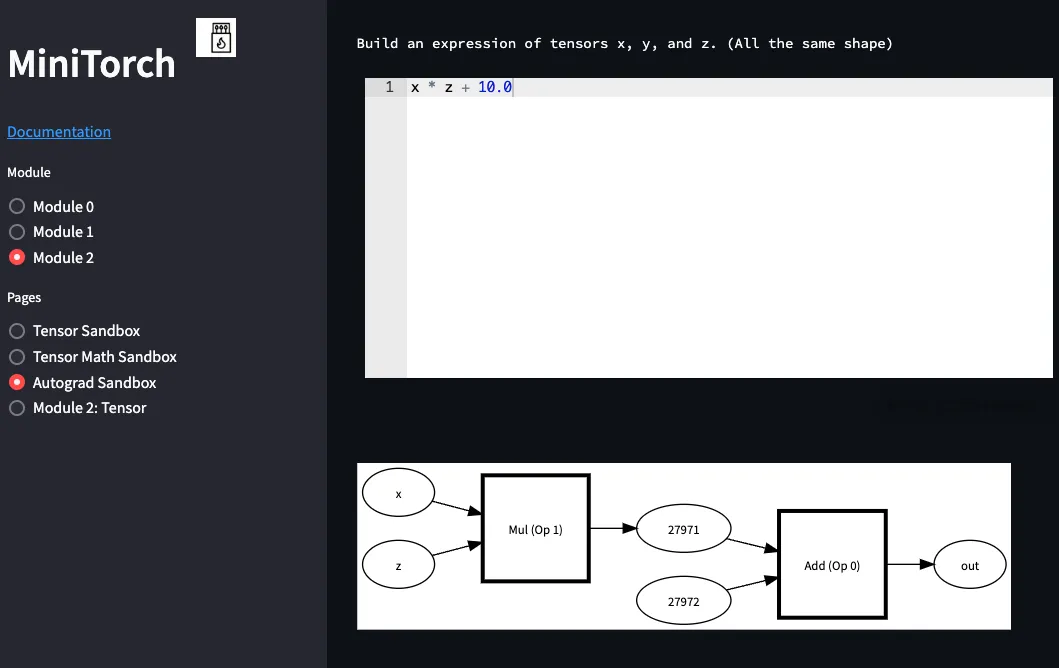
We have built a debugging tool for you to observe the workings of your expressions to see how the graph is built. You can alter the expression at in Streamlit to view the graph

y = x * z + 10.0

>>> streamlit run project/app.py -- 2

Todo

First in the tensor_ops.py file you need to implement these three core functions. See the docs for detailed explanations.

`minitorch.tensor_ops.tensor_map(fn: Callable[[float], float]) -> Callable[[Storage, Shape, Strides, Storage, Shape, Strides], None]`

Low-level implementation of tensor map between tensors with possibly different strides.

Simple version:

Fill in the out array by applying fn to each value of in_storage assuming out_shape and in_shape are the same size.

Broadcasted version:

Fill in the out array by applying fn to each value of in_storage assuming out_shape and in_shape broadcast. (in_shape must be smaller than out_shape).

Parameters:

fn (Callable[[float], float]) –

function from float-to-float to apply

Returns:

Callable[[Storage, Shape, Strides, Storage, Shape, Strides], None] –

Tensor map function.

`minitorch.tensor_ops.tensor_zip(fn: Callable[[float, float], float]) -> Callable[[Storage, Shape, Strides, Storage, Shape, Strides, Storage, Shape, Strides], None]`

Low-level implementation of tensor zip between tensors with possibly different strides.

Simple version:

Fill in the out array by applying fn to each value of a_storage and b_storage assuming out_shape and a_shape are the same size.

Broadcasted version:

Fill in the out array by applying fn to each value of a_storage and b_storage assuming a_shape and b_shape broadcast to out_shape.

Parameters:

fn (Callable[[float, float], float]) –

function mapping two floats to float to apply

Returns:

Callable[[Storage, Shape, Strides, Storage, Shape, Strides, Storage, Shape, Strides], None] –

Tensor zip function.

`minitorch.tensor_ops.tensor_reduce(fn: Callable[[float, float], float]) -> Callable[[Storage, Shape, Strides, Storage, Shape, Strides, int], None]`

Low-level implementation of tensor reduce.

out_shape will be the same as a_shape except with reduce_dim turned to size 1

Parameters:

fn (Callable[[float, float], float]) –

reduction function mapping two floats to float

Returns:

Callable[[Storage, Shape, Strides, Storage, Shape, Strides, int], None] –

Tensor reduce function.

Todo

Next implement the forward version of the tensor_functions.py file.

Mul
Sigmoid
ReLU
Log
Exp
Sum (with dim arg)
LT
EQ
IsClose (no backward)
Permute

Todo

Finally add functions in minitorch/tensor.py for each of the following, and pass tests marked as task2_3. You need to implement many of the same functions from minitorch/scalar.py.

Properties: - size - dims

Operators (you will likely find _ensure_tensor useful here since the user may pass in standard python values):

add
sub
mul
lt
eq
gt
neg
radd
rmul
all
is_close
sigmoid
relu
log
exp

Should take an optional dim argument:

sum
mean
permute
view

Should set .grad to None - zero_grad_

Tasks 2.4: Gradients and Autograd

Similar to minitorch.Scalar, minitorch.Tensor is a Variable that supports autodifferentiation. In this task, you will implement backward functions for tensor operations.

Todo

Implement the backward functions in minitorch/tensor_functions.py, and pass tests marked as task2_4.

Task 2.5: Training

If your code works you should now be able to move on to the tensor training script in project/run_tensor.py. This code runs the same basic training setup as in module1, but now utilize your tensor code.

Todo

Implement a neural network over the data with three linears (2-> Hidden (relu), Hidden -> Hidden (relu), Hidden -> Output (sigmoid)). It should do exactly the same thing as the corresponding functions in project/run_scalar.py, but now use the tensor code base.

Train a tensor model and add your results for all datasets to the README.
Record the time per epoch reported by the trainer. (It is okay if it is slow).