Fundamentals

This introductory module is focused on introducing several core software engineering methods for testing and debugging, and also includes some basic mathematical foundations.

Before starting this assignment, make sure to set up your workspace following the setup guide, to understand how the code should be organized.

Guides

Each module has a set of guides to help with the background material. We recommend working through the assignment and utilizing the guides suggested for each task.

• Contributing
• Functional Python
• Property Testing
• Modules
• Visualization

Task 0.1: Operators

This task is designed to help you get comfortable with style checking and testing. We ask you to implement a series of basic mathematical functions. These functions are simple, but they form the basis of MiniTorch. Make sure that you understand each of them as some terminologies might be new.

Todo

Complete the following functions in minitorch/operators.py and pass tests marked as task0_1.

minitorch.operators.mul(x: float, y: float) -> float

\(f(x, y) = x * y\)

minitorch.operators.id(x: float) -> float

\(f(x) = x\)

minitorch.operators.eq(x: float, y: float) -> float

\(f(x) =\) 1.0 if x is equal to y else 0.0

minitorch.operators.neg(x: float) -> float

\(f(x) = -x\)

minitorch.operators.add(x: float, y: float) -> float

\(f(x, y) = x + y\)

minitorch.operators.max(x: float, y: float) -> float

\(f(x) =\) x if x is greater than y else y

minitorch.operators.lt(x: float, y: float) -> float

\(f(x) =\) 1.0 if x is less than y else 0.0

minitorch.operators.sigmoid(x: float) -> float

\(f(x) = \frac{1.0}{(1.0 + e^{-x})}\)

(See https://en.wikipedia.org/wiki/Sigmoid_function )

Calculate as

\(f(x) = \frac{1.0}{(1.0 + e^{-x})}\) if x >=0 else \(\frac{e^x}{(1.0 + e^{x})}\)

for stability.

minitorch.operators.relu(x: float) -> float

\(f(x) =\) x if x is greater than 0, else 0

(See https://en.wikipedia.org/wiki/Rectifier_(neural_networks) .)

minitorch.operators.inv(x: float) -> float

\(f(x) = 1/x\)

minitorch.operators.inv_back(x: float, d: float) -> float

If \(f(x) = 1/x\) compute \(d \times f'(x)\)

minitorch.operators.relu_back(x: float, d: float) -> float

If \(f = relu\) compute \(d \times f'(x)\)

minitorch.operators.log_back(x: float, d: float) -> float

If \(f = log\) as above, compute \(d \times f'(x)\)

minitorch.operators.is_close(x: float, y: float) -> float

\(f(x) = |x - y| < 1e-2\)

Task 0.2: Testing and Debugging

We ask you to implement property tests for your operators from Task 0.1. These tests should ensure that your functions not only work but also obey high-level mathematical properties for any input. Note that you need to change arguments for those test functions.

Todo

Complete the test functions in tests/test_operators.py marked as task0_2.

Task 0.3: Functional Python

To practice the use of higher-order functions in Python, implement three basic functional concepts. Use them in combination with operators described in Task 0.1 to build up more complex mathematical operations that work on lists instead of single values.

Todo

Complete the following functions in minitorch/operators.py and pass tests marked as tasks0_3.

minitorch.operators.map(fn: Callable[[float], float]) -> Callable[[Iterable[float]], Iterable[float]]

Higher-order map.

See https://en.wikipedia.org/wiki/Map_(higher-order_function)

Parameters:

• fn (Callable[[float], float]) –

  Function from one value to one value.

Returns:

• Callable[[Iterable[float]], Iterable[float]] –

  A function that takes a list, applies fn to each element, and returns a

• Callable[[Iterable[float]], Iterable[float]] –

  new list

minitorch.operators.negList(ls: Iterable[float]) -> Iterable[float]

Use map and neg to negate each element in ls

minitorch.operators.zipWith(fn: Callable[[float, float], float]) -> Callable[[Iterable[float], Iterable[float]], Iterable[float]]

Higher-order zipwith (or map2).

See https://en.wikipedia.org/wiki/Map_(higher-order_function)

Parameters:

• fn (Callable[[float, float], float]) –

  combine two values

Returns:

• Callable[[Iterable[float], Iterable[float]], Iterable[float]] –

  Function that takes two equally sized lists ls1 and ls2, produce a new list by

• Callable[[Iterable[float], Iterable[float]], Iterable[float]] –

  applying fn(x, y) on each pair of elements.

minitorch.operators.addLists(ls1: Iterable[float], ls2: Iterable[float]) -> Iterable[float]

Add the elements of ls1 and ls2 using zipWith and add

minitorch.operators.reduce(fn: Callable[[float, float], float], start: float) -> Callable[[Iterable[float]], float]

Higher-order reduce.

Parameters:

• fn (Callable[[float, float], float]) –

  combine two values

• start (float) –

  start value \(x_0\)

Returns:

• Callable[[Iterable[float]], float] –

  Function that takes a list ls of elements

• Callable[[Iterable[float]], float] –

  \(x_1 \ldots x_n\) and computes the reduction :math:`fn(x_3, fn(x_2,

• Callable[[Iterable[float]], float] –

  fn(x_1, x_0)))`

minitorch.operators.sum(ls: Iterable[float]) -> float

Sum up a list using reduce and add.

minitorch.operators.prod(ls: Iterable[float]) -> float

Product of a list using reduce and mul.

Task 0.4: Modules

This task is to implement the core structure of the :class:minitorch.Module class. We ask you to implement a tree data structure that stores named :class:minitorch.Parameter on each node. Such a data structure makes it easy for users to create trees that can be walked to find all of the parameters of interest.

To experiment with the system use the Module Sandbox:

>>> streamlit run app.py -- 0

Todo

Complete the functions in minitorch/module.py and pass tests marked as tasks0_4.

minitorch.module.Module.train() -> None

Set the mode of this module and all descendent modules to train.

minitorch.module.Module.eval() -> None

Set the mode of this module and all descendent modules to eval.

minitorch.module.Module.named_parameters() -> Sequence[Tuple[str, Parameter]]

Collect all the parameters of this module and its descendents.

Returns:

• Sequence[Tuple[str, Parameter]] –

  The name and Parameter of each ancestor parameter.

minitorch.module.Module.parameters() -> Sequence[Parameter]

Enumerate over all the parameters of this module and its descendents.

Task 0.5: Visualization

For the first few assignments, we use a set of datasets implemented in minitorch/datasets.py, which are 2D point classification datasets. (See TensorFlow Playground for similar examples.) Each of these dataset can be added to the visualization.

To experiment with the system use:

streamlit run app.py -- 0

Read through the code in project/run_torch.py to get a sneak peek of an implementation of a model for these datasets using Torch.

You can also provide a model that attempts to perform the classification by manipulating the parameters.

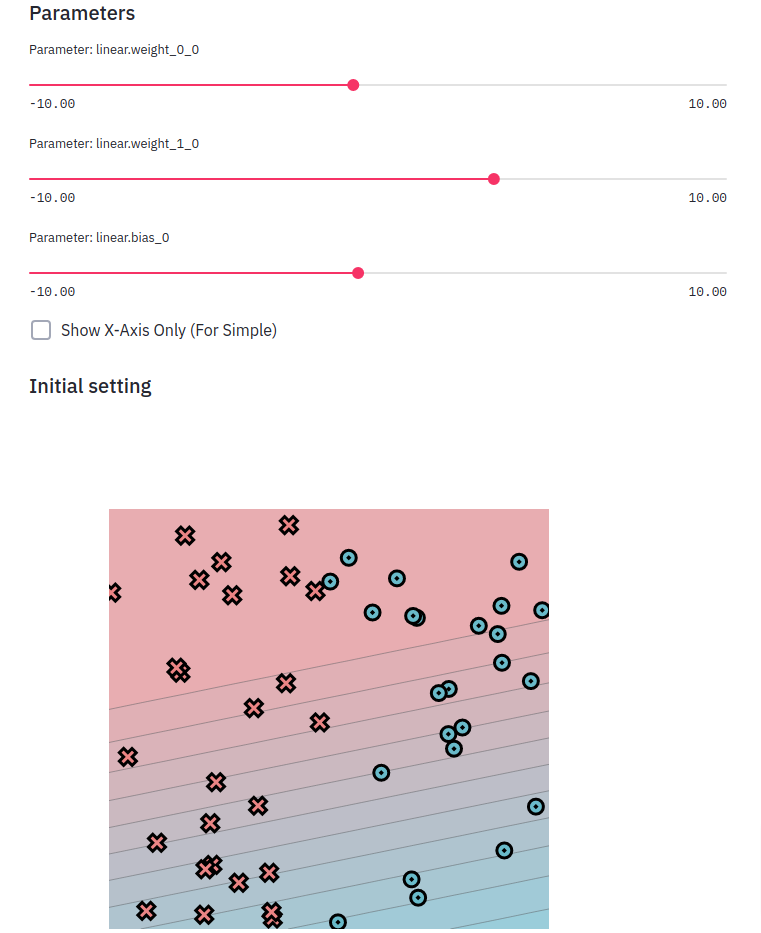
Todo

Start a streamlit server and print an image of the dataset. Hand-create classifiers that split the linear dataset into the correct colors.

Add the image in the README file in your repo along with the parameters that your used.